O que é um Caixeiro Viajante?

Contexto Histórico

Imagine um tipo de vendedor que não fica esperando você chegar à loja, mas vai até você, esteja você em casa, na empresa ou até mesmo naquele cantinho afastado no meio do nada. O caixeiro-viajante é o mercador ambulante que vende produtos fora das regiões onde eles são produzidos, isto é, que percorre as ruas e estradas a vender seus produtos, principalmente manufaturados. Uma antiga profissão, tornou-se fundamental em uma época em que não havia facilidade do transporte entre cidades; os caixeiros-viajantes eram então a única forma de transportar produtos entre diferentes regiões fora das grandes cidades. Comercializavam uma vasta categoria de produtos, visitavam residências, empresas e lojas em cidades, vilarejos e fazendas. Precisavam viajar longas distâncias e ter habilidades de comunicação e persuasão para negociar seus produtos. Eram os verdadeiros artistas da negociação, precisando dominar a arte da comunicação e persuasão para convencer as pessoas a comprarem seus produtos.

Há uma publicação da Universidade Estadual do Maranhão, que relata alguns detalhes interessantes do contexto histórico deste afamado vendedor. A Publicação é uma dissertação de Mestrado Profissional, que tem o título: Cultura material e imaterial do Caixeiro Viajante Recomendo a leitura!

O caixeiro viajante vestia bota de cano alto, conhecida por Musterreiter Stüfel, provida de grandes esporas, bombacha, mais apropriada para semanas de cavalgadas, camisa xadrez, lenço ao pescoço e chapéu de aba larga para proteção contra a canícula, além do poncho ou capa de chuva - que A. J. Renner logrou impermeabilizar na década de 1880, especialmente para o caixeiro viajante, que também ele foi. Completava a indumentária o relho de cabo curto na mão direita e guaiaca na cintura, onde guardava o dinheiro e também a pistola (FLORES, 2000 apud MÜHLEN, 2018, p. 125)

Recomendo também este episódio do programa A Praça é Nossa, exibido pelo SBT. Nos primeiros minutos desse programa, os humoristas Giovanni Braz e Carlos Alberto de Nóbrega definem, de forma bem-humorada, esta antiga profissão.

Contexto Matemático

O problema do Caixeiro Viajante, ou Travelling Salesman Problem - TSP, é um problema clássico da otimização em matemática e da ciência da computação, que consiste em encontrar o menor caminho que permite visitar um conjunto de cidades e retornar à cidade de origem. O problema pode ser expresso matematicamente como um problema de programação linear inteira, no qual a função objetivo é a soma das distâncias entre as cidades visitadas e as restrições impõem que cada cidade seja visitada exatamente uma vez e que o percurso termine na cidade de origem.

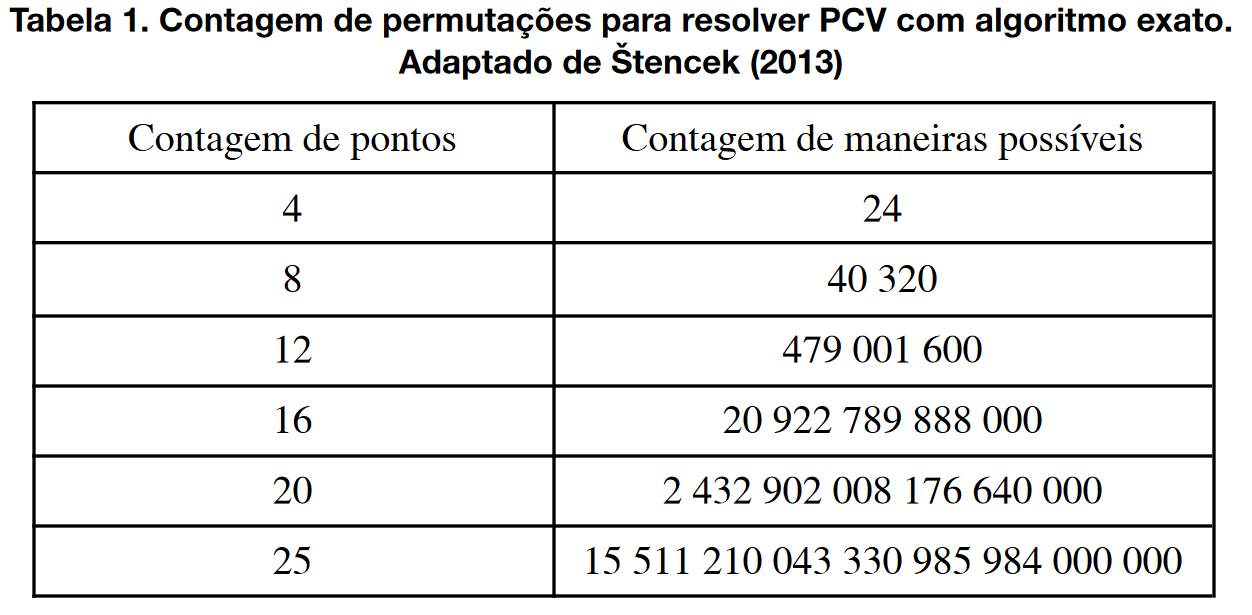
Quando o de pontos N (“cidades”) é pequeno, o problema pode ser resolvido por meio de força bruta, listando todas as rotas possíveis para conferir qual é a mais curta. Mas isso logo se torna inviável quando N aumenta, mesmo com computadores poderosos, porque o número de rotas possíveis é dado pelo fatorial N! = 1 x 2 x … x N, o qual cresce muito rapidamente.

Na Tabela abaixo, é possível verificar que no caso de poucos pontos (vértices) o problema do caixeiro viajante não é tão complicado, porém, quando o problema tem mais pontos, a contagem dos caminhos possíveis já é um número enorme. No caso de 20 pontos é uma quantidade tão grande de cálculos que é impossível resolvê-lo em tempo real.

O problema do Caixeiro Viajante é um exemplo de problema de otimização combinatória, no qual a solução ótima é obtida através da avaliação de todas as possíveis rotas e seleção daquela com o menor custo. Como o número de possíveis rotas cresce exponencialmente com o número de cidades, o problema do Caixeiro Viajante é considerado um problema NP-difícil, o que significa que é muito difícil encontrar uma solução ótima em tempo hábil para problemas com um grande número de cidades.

Existem diversas técnicas matemáticas e algoritmos de otimização que podem ser utilizados para resolver o problema do Caixeiro Viajante, como algoritmos genéticos, meta-heurísticas, programação dinâmica, entre outros. A escolha do método depende do tamanho do problema, da complexidade das restrições e da qualidade desejada da solução.

Métodos Exatos

Busca Exaustiva ou Força Bruta

Um dos métodos exatos mais comuns e até intuitivos para resolver o TSP é conhecido como Busca Exaustiva ou Força Bruta. Esse método envolve uma abordagem que consiste na minuciosa avaliação de todas as possíveis soluções até encontrar a ótima. Em sua aplicação, todas as combinações são consideradas de forma exaustiva a fim de compará-las e, finalmente, determinar a solução mais adequada. Porém, como vimos acima, o crescimento exponencial do problema torna inviável a adoção deste modelo para um grande número de cidades (instâncias).

Branch and Bound (Ramificação e Poda)

O Branch and Bound, em tradução direta, ramificação e poda, consiste em O método Branch and Bound inicia abordando o problema original como um único subproblema. Em seguida, esse subproblema é sistematicamente dividido em dois ou mais subproblemas menores, frequentemente fixando valores de variáveis. O processo se repete de forma contínua, até que até que todos os subproblemas se tornem triviais, possuindo apenas uma solução possível. Essa estratégia visa explorar seletivamente partes promissoras do espaço de solução, otimizando a busca por uma solução ótima de maneira eficiente.

Métodos Heurísticos

KNN - K-Nearest Neighbors

O KNN (K-Nearest Neighbors) é um algoritmo de aprendizado de máquina que pode ser adaptado para resolver o TSP. A ideia principal é usar a similaridade entre cidades para construir uma rota eficiente.

A partir desse ponto de partida, o algoritmo seleciona o próximo vértice (ou cidade) que tem o menor peso, ou seja, a menor distância para o vértice atual. o processo de seleção do próximo vértice é repetido iterativamente até que todos os vértices mais próximos tenham sido adicionados à solução. Esse procedimento segue a lógica de minimização das distâncias, evitando repetições. Ao final do processo, o ponto inicial (cidade de partida) é reintroduzido ao roteiro para completar o circuito, assegurando que a solução final seja um circuito Hamiltoniano.

K-opt

O k-opt é uma técnica de otimização, frequentemente aplicada ao TSP, usada para aprimorar soluções iniciais aproximadas. A lógica do método é realizar modificações em uma solução existente, alterando as conexões entre as cidades visitadas. O valor de k se refere ao número de conexões que são modificadas em cada iteração, diferentes valores de k podem obter diferentes níveis de otimização. O processo de aplicação, em regra, envolve uma solução inicial para o TSP, que pode ser obtida por meio outras heurísticas, como por exemplo o KNN, ou ainda outras abordagens aproximadas. O valor de "k" é determinado, especificando quantas conexões devem ser modificadas em cada iteração. Valores comuns para k incluem 2-opt, modificando duas arestas de cada vez, ou 3-opt, modificando três arestas de cada vez, e assim por diante.

2-opt

O algoritmo 2-opt é uma técnica que opera na troca de duas arestas não adjacentes em um circuito (ou caminho) para obter uma solução melhor. A ideia principal é inverter a ordem das cidades entre duas arestas, removendo assim a interseção no caminho, o que pode reduzir o comprimento total do percurso.

3-opt

O 3-opt é uma extensão do 2-opt e opera de maneira semelhante, mas envolve a troca de três arestas em vez de duas. Ele é mais complexo, pois existem várias combinações possíveis de trocas de três arestas, tornando-o mais eficaz na melhoria de soluções, mas também mais computacionalmente intensivo. O 3-opt é frequentemente aplicado em problemas TSP para tentar encontrar soluções ainda melhores do que as obtidas com o 2-opt.

Ambos os algoritmos são técnicas heurísticas e trabalham de maneira incremental, modificando a solução existente para buscar uma melhoria local. Eles não garantem a obtenção da solução ótima global, mas são eficazes para refinar soluções em problemas práticos.